Разностные схемы для гиперболических задач

Потеря монотонности разностной схемы характерна в той или иной степени для всех схем повышенного порядка аппроксимации. Для преодоления немонотонности численного решения схем высокого порядка используют так называемые гибридные разностные схемы. Они относятся к классу нелинейных, в них, на основе анализа поведения решения, производится переключение на монотонные схемы первого порядка в зонах, где… Читать ещё >
Разностные схемы для гиперболических задач (реферат, курсовая, диплом, контрольная)
Разностные схемы для уравнения переноса
Рассмотрим задачу Коши для уравнения вида.
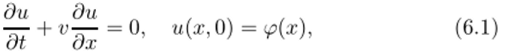
в которой скорость переноса v может быть функцией х. Для уравнения (6.1) можно предложить множество разностных схем, различающихся порядком аппроксимации, способом представления производных и т. д. Остановимся вначале на явных разностных схемах, в которых каждое уравнение системы содержит лишь одну неизвестную величин}', что позволяет последовательно вычислить значения решения на новом временном слое.
Известно, что важнейшим свойством, которым должны обладать явные разностные схемы, является устойчивость способность схемы не накапливать вычислительные возмущения. Устойчивость схемы необходимое требование для обеспечения сходимости разностного решения к точному. Для гиперболического уравнения обычно проводится анализ устойчивости по начальным данным на основе спектра собственных чисел оператора перехода к новому временному слою, исходя из которого выбираются приемлемые для расчетов разностные схемы. Так, симметричная разностная схема.
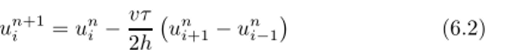
имеет очень жесткое условие устойчивости (т2 < vh) и нс используется для практических алгоритмов. Разностные схемы.
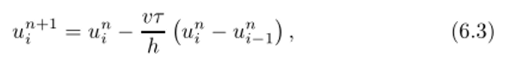
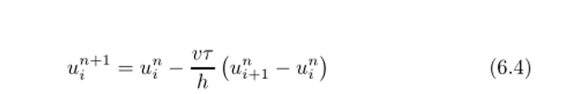

являются условно устойчивыми. Для обеспечения их устойчивости необходимо, во-первых, выполнение условия Куранта Фридрихса — Леви (КФЛ):
а во-вторых, использование разностей навстречу потоку, т. е. применение схемы (6.3) при V > 0 и (6.4) при v < 0.
Явная схема с разностями навстречу потоку. Если мы будем избирательно применять две предыдущие схемы, а именно, при v > > 0 схему (6.3), а при v < 0 схему (6.4), то разностная схема.
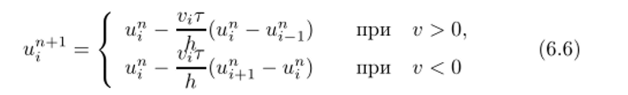
будет безразлична к направлению скорости и устойчива при условии v /h ^ 1. Нетрудно заметить, что односторонние разности в этой схеме берутся навстречу потоку (говорят, что схема обладает свойством mpanenopmuenoemu). Схем}' такого вида называют противопоточной или схемой с разностями навстречу потоку.
В случае уравнения с постоянным значением скорости переноса проблем с конструированием противопоточной разностной схемы нет. Выбирается соответствующая знаку скорости переноса разность, которая используется во всех узлах расчетной области. Условие (6.5) накладывает ограничение на соотношение шагов расчетной сетки. Обычно при заданном шаге по пространству из соотношения (6.5) определяют допустимый временной шаг т < h/v.
Но если скорость переноса является функцией координаты (или времени), то выбор вида разностной аппроксимации необходимо осуществлять на основе анализа знака скорости переноса, например применяя условный оператор. Кроме гот, при переменной скорости переноса v = v (x) условие устойчивости нужно проверить для всех узлов сетки и из этого множества значений временного шага выбрать минимальный: т min,; h/vj.
В работе Куранта с соавторами (1952) был предложен интересный метод конструирования противопоточной схемы, в котором не использовался условный оператор. Важно отметить, что это не просто формальный прием, а подход, содержащий глубокие идеи, на основе которых можно сопоставлять и находить соответствие между противопоточными (несимметричными) и симметричными разностными схемами. К этому близка идея расщепления операторов разностных схем.
Представим скорость переноса в виде суммы ее положительной и отрицательной составляющих:
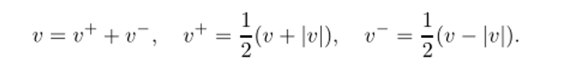
Это позволит представить оператор переноса в виде суммы двух операторов:
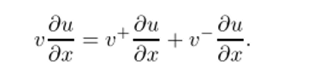
Теперь каждый из операторов имеет знакопостоянный коэффициент, что позволяет применить к нему противопоточную разностную аппроксимацию. Отметим, что разностная схема навстречу потоку для аппроксимации конвективных членов широко используется в различных задачах вычислительной гидродинамики. Часто применяется следующая запись вычислительного алгоритма по схеме (6.6):
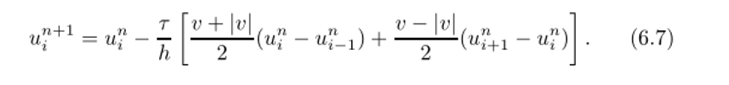
Если мы теперь в правой части (6.7) проведем элементарные преобразования и выделим симметричную разностную производную, то эта схема представится в виде.
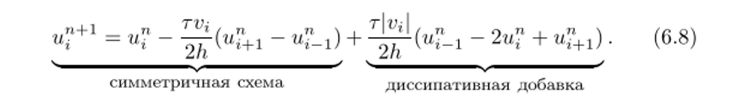
Можно сделать вывод, что нротивопоточная разностная схема (6.7) эквивалентна симметричной (6.2), в которую введена диссипативная добавка, обеспечивающая условную устойчивость схемы.
Схема Лакса. Эта схема была введена в практику вычислений на заре развития вычислительной газодинамики. II хотя упоминания о схеме такого типа встречались в работах разных авторов, общественное мнение связывает ее с именем американского математика Лакса (Lax, P.D.), опубликовавшего в 50-е годы серию работ по различным аспектам теории разностных схем. Применительно к уравнению переноса (6.1) эта схема имеет вид.
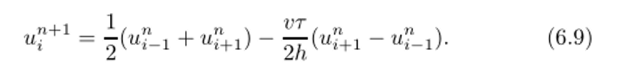
Особенность схемы состоит в том, что для обеспечения ее устойчивости в аппроксимации производной, но времени значение сеточной функции в узле (г, п) заменяется на полусумму значений в соседних узлах того же временного слоя. Эта операция обеспечивает при центральной аппроксимации пространственной производной условную устойчивость разностной схемы (при выполнении условия Куранта — Фридрихса — Леви v /h ^ 1).
Хотя здесь производная по х представлена со вторым порядком аппроксимации, схема из-за специфического представления временнбй производной обладает значительной диссипацией. Это хорошо видно из первого дифференциального приближения:
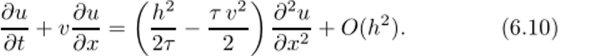
Коэффициент, стоящий в правой части перед второй производной, можно трактовать как коэффициент схемной вязкости. После простых преобразований эту величину можно представить как.
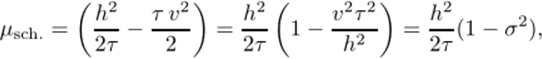
где через а обозначено число Куранта. Из дифференциального приближения можно определить многие свойства этой схемы:
- — схема становится недиссипативной при числе Куранта, равном единице;
- — схема не чувствительна к направлению потока;
при числе Куранта, меньшем единицы, схемная вязкость оказывает стабилизирующее воздействие (положительный коэффициент диффузии), при числе Куранта, большем единицы, коэффициент схемной вязкости становится отрицательным, что приводит к обострению процесса диффузии и, в конечном счете, к потере вычислительной устойчивости схемы;
— при уменьшении шага по времени диссипативные свойства схемы растут.
В числе перечисленных особенностей есть и такие, которые существенно снижают достоинства схемы. Однако простота алгоритма часто является основанием для ее использования на начальных (отладочных) шагах построения расчетных программ. Кроме этого, схема Лакса, как мы увидим далее, является составной частью эффективных многошаговых алгоритмов, в которых с ее помощью выполняется предварительный шаг (шаг прогноза).
Схемы второго порядка. Разностные схемы, рассмотренные ранее, были схемам первого порядка (по пространственной или временной переменной). При построении схем второго порядка необходимо обеспечить повышенный порядок аппроксимации как по пространственной, гак и, но временной переменой. Рассмотрим несколько схем такого типа.
Схема «чехарда». Схема второго порядка как по пространственной переменной, так и по времени простейшего типа может быть представлена в виде.

Эту схему называют схемой с перешагиванием, но больше она известна под названием «чехарда» (leap-frog scheme). Схема является трехслойиой и строит решение по двум предыдущим временным слоям. Поэтому при ее применении возникают проблемы с началом вычислений, которое должно осуществляться каким либо другим методом.
Схема Лакса — Вендроффа. Одной из наиболее известных схем такого типа является центральная схема, называемая по имени ее авторов, схемой Лакса — Вендроффа. Она заняла определенную нишу в теории разностных схем для гиперболических уравнений, с ней связано много весьма продуктивных идей, но основное ее достоинство состоит в том, что она легко обобщается и переносится на случай более сложных задач — задач течения сжимаемого газа, описываемых системами квазилинейных уравнений, где она достаточно долгое время была одним из основных вычислительных инструментов.
Полезно изучить особенности этой схемы на примере применения ее к уравнению переноса вида (6.1). Для построения схемы второго порядка выпишем формулу Тейлора:
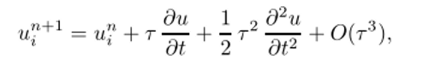
которую будем рассматривать совместно с исходным уравнением (6.1) Это уравнение будем использовать для того, чтобы заменить в разложении временные производные пространственными. Это возможно, так как первая производная, но времени выражается непосредственно из (6.1): du/dt = —vdu/dx. Вторая производная также легко находится из следующей цепочки соотношений: 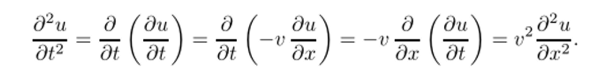
Заметим, что это представление является точным лишь при постоянной скорости переноса: v = const. В противном случае оно носит приближенный характер, однако, если скорость переноса v (x) достаточно гладкая функция, его можно использовать для преобразований разностных соотношений, которые носят локальный характер.
Подставляя полученные с помощью исходного дифференциального уравнения выражения для производных в приведенную выше формулу Тейлора, получим соотношение.
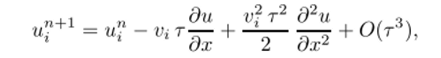
а заменяя производные по пространству конечноразностными соотношениями второго порядка, получим (после некоторых простых преобразований) разностную схему.

называемую схемой Лакса Вендроффа. Эта схема была введена в практику вычислений вместе с рядом других в серии работ, опубликованных Лаксом и Всндроффом в 1960;1964 гг.
Двухшаговый вариант схемы Лакса — Вендроффа. Позже Рихтмайер предложил оригинальный двухшаговый вариант схемы, который из-за удобства в реализации долгое время был одним из основных вычислительных алгоритмов газодинамики. Приведем этот вариант.
На первом полушаге вычислим промежуточное значение решения по простой схеме Лакса первого порядка. Этому промежуточному значению припишем верхний индекс п + ½ и будем иметь в виду, что используется также половинный шаг по времени. Применяя эту схему, получим значения решения на промежуточном временном слое: t = tn+l/2. При этом отметим, что из-за применения схемы Лакса, в которой на нижнем слое отсутствует центральный узел, решение воспроизводится на промежуточном слое также в системе полуцелых точек.
Приведем запись разностных соотношений для двух соседних промежутков:
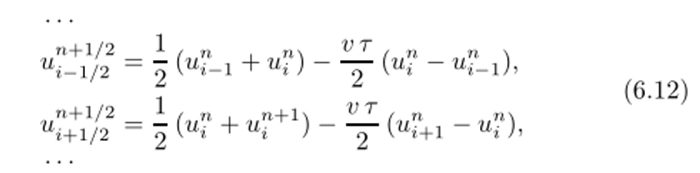
Второй полушаг состоит в вычислении решения на новом временном слое п + 1 на основе схемы с центральными разностями как по пространству, так и по времени — схемы «крест». Для вычисления пространственных производных используются значения решения на промежуточном слое в системе полуцелых точек, само решение восстанавливается в той же самой системе точек, в которой оно было определено к началу временного шага:
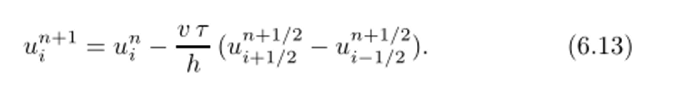
Соотношения (6.12) и (6.13) вместе определяют двухшаговую схему Лакса — Веидроффа. На первом ее этапе обеспечивается выполнение условий устойчивости. Этот этап называют иногда предиктором. Второй этап обеспечивает выполнение требуемой точности, и его называют корректором. Методы предиктора-корректора часто используются в вычислительной математике, при этом этап корректора может включать в себя итерационный блок.
Можно легко показать, что, исключая из (6.13) промежуточные значения, с помощью соотношений (6.12) мы приходим к основному — одиошаговому — варианту схемы. В смысле порядка аппроксимации и устойчивости оба варианта эквивалентны, но двухшаговый более удобен при проведении вычислений, поэтому именно с ним связывается обычно наименование этой разностной схемы. Двухшаговый вариант особенно удобно использовать при построении разностных схем для более сложных задач, в частности для систем квазилинейных уравнений нестационарной газодинамики.
Монотонность решения в схемах второго порядка. Последний член в правой части (6.11) имеет вид, отличный от вида диссипативных членов схем первого порядка (6.8) и (6.10). В данном случае он обеспечивает подавление ошибки, связанной с первым порядком аппроксимации производной по времени. Таким образом, данная схема является схемой второго порядка как, но времени, гак и, но пространственной переменной. Ее первое дифференциальное приближение уже не будет содержать диссипативный член, но в нем будет присутствовать дисперсионная составляющая с третьей производной, которая является причиной фазовых ошибок схемы. Можно ожидать, что данная схема будет слабо размазывать решение, но в области его резкого изменения могут появляться нефизические осцилляции, вызванные дисперсией.
Разностная схема, которая переводит решение, имеющее вид монотонной функции продольной координаты, в монотонное же решение, называется монотонной разностной схемой. Согласно этому определению, схема Лакса — Веидроффа является немонотонной.
С.К. Годуновым была установлена теорема о монотонности, занимающая одно из центральных мест в теории разностных схем. Согласно этой теореме, для линейного уравнения вида (6.1) не существует монотонных схем с порядком выше первого.
Потеря монотонности разностной схемы характерна в той или иной степени для всех схем повышенного порядка аппроксимации. Для преодоления немонотонности численного решения схем высокого порядка используют так называемые гибридные разностные схемы. Они относятся к классу нелинейных, в них, на основе анализа поведения решения, производится переключение на монотонные схемы первого порядка в зонах, где фазовые ошибки проявляются особо сильно, и возвращение к схемам высокого порядка в областях гладкого изменения решения.
Схема Мак-Кормака. Это также двухшаговая схема второго порядка, безразличная к направлению потока. Ее более удобно продемонстрировать на консервативной форме уравнения переноса:
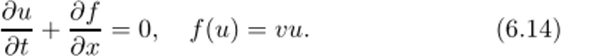
Схема состоит из двух последовательно выполняемых шагов:
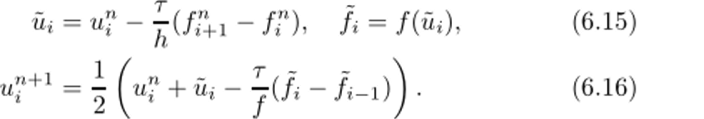
На первом этапе (6.15) находят предварительное значение решения щ в узлах сетки на основе односторонней разностной схемы. По найденному таким образом решению вычисляют предварительные значения потоков /г. Далее, на основе односторонних схем, имеющих противоположное направление (6.16), определяется решение на следующем временном слое.
Этот алгоритм допускает различные модификации, он хорошо адаптируется к решению как квазилинейных систем, так и многомерных гиперболических задач. В 1970;е годы эта схема была одной из основных разностных схем зарубежных (в основном американских) вычислителей, но в настоящее время она вытеснена более современными, основанными на идеях гибридизации.